PDF: “A Mathematician’s Lament”
This “book” wasn’t so much a book as it was a long essay; nonetheless, I’m archiving it under my bookNotes tag. The essay is a lament on the state of mathematics education, but I think it’s quite applicable to many disciplines of education (including tech). The author explains the dilemma thus:
If I had to design a mechanism for the express purpose of destroying a child’s natural curiosity and love of pattern-making, I couldn’t possibly do as good a job as is currently being done—I simply wouldn’t have the imagination to come up with the kind of senseless, soul-crushing ideas that constitute contemporary mathematics education.
However, the author argues that if mathematics education (and I would suggest tech) were based more in the history, philosophy, and art of the underlying principles of the discipline, then learning it through practice would probably be a lot more fun than it often is.
There is such breathtaking depth and heartbreaking beauty in [the] ancient art form [of mathematics]. How ironic that people dismiss [it] as the antithesis of creativity. They are missing out on an art form older than any book, more profound than any poem, and more abstract than any abstract…We could all be having so much more fun.
I think the spirit of technology—specifically building for the web—retains some of the art behind the form. There’s still a lot of people doing work on the web who didn’t learn it through any kind of standardized education. They learned it through tinkering ans experimentation because it was simply fun to do. But as more and more people learn “to code” as a kind of trade, perhaps we should be very wary of trodding the same educational path math has taken. If “writing code” is merely banging out something until the computer compiles and runs it, we’re likely to end up in a similar situation as math where the “rich and fascinating adventure of the imagination has been reduced to a sterile set of...procedures”.
An Example of the Beauty of Ideas in Mathematics
The author illustrates the beauty of ideas in mathematics by showing a simple drawing of a rectangle with a triangle inside of it and asking the question: how can you figure out how much space that triangle takes up inside of that rectangle?
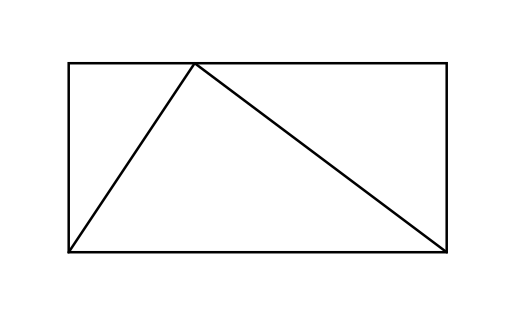
At first—at least for me—it’s quite unapparent how to solve the problem. Then the author draws one more line on the diagram which cuts the triangle in half and instantly reveals the solution! The triangle takes up exactly half of the space in the rectangle (each sub-rectangle being equally divided diagonally by the sides of the triangle).
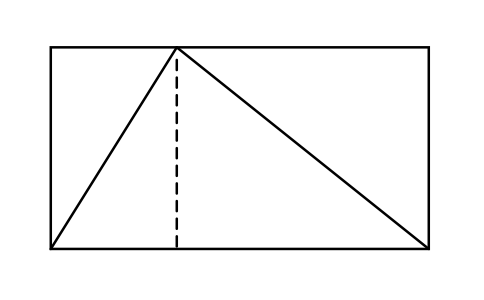
It’s an fascinating visual exercise, because at first you have no idea how to approach the problem. Then, through the help of the author, you realize how elegant the answer actually is through the process of simply drawing one more line on the diagram.
Now where did this idea of mine come from? How did I know to draw that line? How does a painter know where to put his brush? Inspiration, experience, trial and error, dumb luck. That’s the art of it, creating these beautiful little poems of thought, these sonnets of pure reason. There is something so wonderfully transformational about this art form. The relationship between the triangle and the rectangle was a mystery, and then that one little line made it obvious. I couldn’t see, and then all of a sudden I could. Somehow, I was able to create a profound simple beauty out of nothing, and change myself in the process. Isn’t that what art is all about?
This is why it is so heartbreaking to see what is being done to mathematics in school. This rich and fascinating adventure of the imagination has been reduced to a sterile set of “facts” to be memorized and procedures to be followed.
From this visual proof, we arrive at an understanding of the formula for the area of a triangle: “A = 1/2B×H, The area of a triangle is equal to one-half its base times its height.” But that’s not what the whole exercise is meant to illustrate.
It’s not about formulas, or memorizing interesting facts. That’s fine in context, and has its place just as learning a vocabulary does—it helps you to create richer, more nuanced works of art. But it’s not the fact that triangles take up half their box that matters. What matters is the beautiful idea of chopping it with the line, and how that might inspire other beautiful ideas and lead to creative breakthroughs in other problems—something a mere statement of fact can never give you.
In other words:
By removing the creative process and leaving only the results of that process, you virtually guarantee that no one will have any real engagement with the subject.
The author then states (emphasis mine):
By concentrating on what, and leaving out why, mathematics is reduced to an empty shell. The art is not in the “truth” but in the explanation, the argument. It is the argument itself which gives the truth its context, and determines what is really being said and meant. Mathematics is the art of explanation. If you deny students the opportunity to engage in this activity—to pose their own problems, make their own conjectures and discoveries, to be wrong, to be creatively frustrated, to have an inspiration, and to cobble together their own explanations and proofs—you deny them mathematics itself.
Miscellaneous Quotes I Liked
On Math Being Fun Because Its Irrelevant to Daily Life
The saddest part of all this “reform” are the attempts to “make math interesting” and “relevant to kids’ lives.” You don’t need to make math interesting — it’s already more interesting than we can handle! And the glory of it is its complete irrelevance to our lives. That’s why it’s so fun!…In any case, do you really think kids even want something that is relevant to their daily lives? You think something practical like compound interest is going to get them excited? People enjoy fantasy, and that is just what mathematics can provide—a relief from daily life, an anodyne to the practical workaday world.
This has been true of programming as well for me. Sure, solving problems at work can be interesting and intellectually stimulating. But the real fun part of it comes on the side projects where I can to dabble in whatever fantasy I want to make the computer come alive. That’s the code that’s a relief from the daily, practical life of coding.
On Good Problems
But a problem, a genuine honest-to-goodness natural human question—that’s another thing. How long is the diagonal of a cube? Do prime numbers keep going on forever? Is infinity a number? How many ways can I symmetrically tile a surface? The history of mathematics is the history of mankind’s engagement with questions like these, not the mindless regurgitation of formulas and algorithms (together with contrived exercises designed to make use of them)…A good problem is something you don’t know how to solve. That’s what makes it a good puzzle, and a good opportunity. A good problem does not just sit there in isolation, but serves as a springboard to other interesting questions
On Utility Not Being the Sole Measurement of Value
Just because a subject happens to have some mundane practical use does not mean that we have to make that use the focus of our teaching and learning. It may be true that you have to be able to read in order to fill out forms at the DMV, but that’s not why we teach children to read. We teach them to read for the higher purpose of allowing them access to beautiful and meaningful ideas.
On Teaching (And I.M.O. Parenting)
Teaching is not about information. It’s about having an honest intellectual relationship with your students. It requires no method, no tools, and no training. Just the ability to be real. And if you can’t be real, then you have no right to inflict yourself upon innocent children...you will never be a real teacher if you are unwilling to be a real person. Teaching means openness and honesty, an ability to share excitement, and a love of learning.
On Ideas Transcending Notations
I would love to see more of this kind of approach in conference talks. I want to hear ideas not implementations. Ideas transcend implementations.
Mathematics is not a language, it’s an adventure. Do musicians “speak another language” simply because they choose to abbreviate their ideas with little black dots? If so, it’s no obstacle to the toddler and her song. Yes, a certain amount of mathematical shorthand has evolved over the centuries, but it is in no way essential. Most mathematics is done with a friend over a cup of coffee, with a diagram scribbled on a napkin. Mathematics is and always has been about ideas, and a valuable idea transcends the symbols with which you choose to represent it. As Gauss once remarked, “What we need are notions, not notations.”
Instead it seems what we often get is just a regurgitation of how-to syntax, “here’s how you put together Lego blocks” instead of “why are Lego blocks so effective in building things? Can they take other shapes or forms?”
The cultural problem is a self-perpetuating monster: students learn about math from their teachers, and teachers learn about it from their teachers, so this lack of understanding and appreciation for mathematics in our culture replicates itself indefinitely. Worse, the perpetuation of this “pseudo-mathematics,” this emphasis on the accurate yet mindless manipulation of symbols, creates its own culture and its own set of values. Those who have become adept at it derive a great deal of self-esteem from their success. The last thing they want to hear is that math is really about raw creativity and aesthetic sensitivity. Many a graduate student has come to grief when they discover, after a decade of being told they were “good at math,” that in fact they have no real mathematical talent and are just very good at following directions. Math is not about following directions, it’s about making new directions.
On Curriculum Without Context
we have a math curriculum with no historical perspective or thematic coherence, a fragmented collection of assorted topics and techniques, united only by the ease in which they can be reduced to step-by-step procedures.
Is it just me, or does that feel like the current state of what I would call “building stuff for the web in 2019”?
On Understanding Your Discipline
If you don’t have enough of a feeling for your subject to be able to talk about it in your own voice, in a natural and spontaneous way, how well could you understand it?
On Context Being King
Questioner: But surely we want all of our students to learn a basic set of facts and skills. That’s what a curriculum is for, and that’s why it is so uniform—there are certain timeless, cold hard facts we need our students to know: one plus one is two, and the angles of a triangle add up to 180 degrees. These are not opinions, or mushy artistic feelings.
Author: On the contrary. Mathematical structures, useful or not, are invented and developed within a problem context, and derive their meaning from that context. Sometimes we want one plus one to equal zero (as in so-called ‘mod 2’ arithmetic) and on the surface of a sphere the angles of a triangle add up to more than 180 degrees. There are no “facts” per se; everything is relative and relational. It is the story that matters, not just the ending.
1 + 1 = 2 seems like such an obvious statement, but even that conclusion is based in a context (as the author points out). For example, is 1 + 1 = 2 always a true statement? Not in the context of a binary number system. In binary, 1 + 1 = 10. As the author says, everything is relative and relational. It’s the story that matters not just the ending.